قانون مساحة متوازي الأضلاع
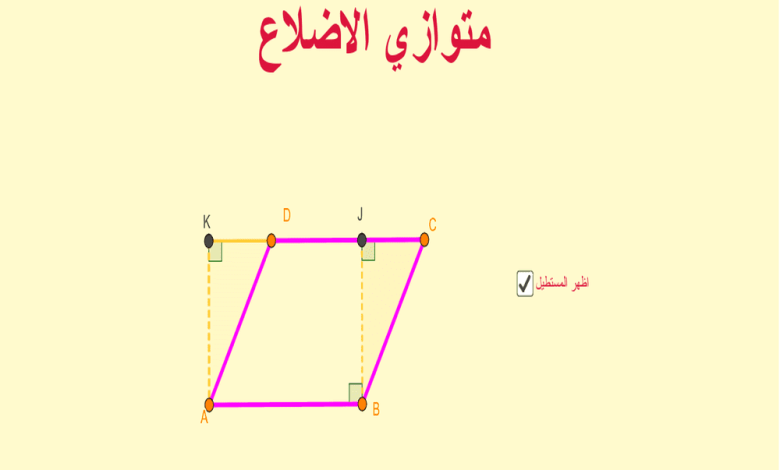
قانون مساحة متوازي الاضلاع متوازي الأضلاع أحد الأشكال الهندسة المميزة الذي دراستها في مجال الهندسة والمعمار، يتميز متوازي الأضلاع أن لديه 4 أضلاع كل ضلعين متساويين ومتوازيين سوف نتعرف عبر موقع الماقه من خلال مقالنا عن قانون المساحة الخاصة متوازي الأضلاع وكل المعلومات التي وردت عنه.
متوازي الأضلاع
- متوازي الأضلاع هو أحد الأشكال الهندسية الإقليمية هو شكل رباعي الأضلاع.
- يحتوي على ضلعين متوازيين، وضلعين متقابلتين قياس أضلاعه تكون متساوية في الطول.
- مجموع زوايا 360 درجة.
خصائص متوازي الأضلاع
يتميز متوازي المستطيلات بمجموعة من الخصائص التي تميزها عن باقي الأشكال الهندسية وهي كالاتي:
- كل زاويتين متواجدين في متوازي الأضلاع متقابلتين متساويتين.
- كل ضلعين متقابلين متوازيين.
- مساحة متوازي الأضلاع تمثل مساحة المثلث في اثنين.
- كل القطر يتواجد في متوازي الأضلاع يقوم بتنظيف متوازي الأضلاع إلى شكلين متساوين.
- يحتوي متوازي الأضلاع على أقطار تكون في مركز الشكل الهندسي ، وتعرف باسم مركز متوازي الأضلاع.
- أي مستقيم يوجد في متوازي الأضلاع ويمر به يقوم بقسم المتوازي إلى شكلين متطابقين.
- كل زاويتين توجد في متوازي الأضلاع متقابلتين متساويتان في القياس.
- مجموع أضلاع متوازي الأضلاع تساوي مجموع مربعين.
- مجموع زاويتين متقابلتين 180 درجة.
الحالات الخاصة في متوازي الأضلاع
يوجد متوازي الأضلاع في بعض الحالات الخاصة وتشمل:
- إذا حدث تعامد في أقطار متوازي المستطيلات أو أطواله بمعنى كل ضلعين متجاورين متساويين ذلك الشكل يعد شكل معين.
- إذا حدث تساوي في أقطار متوازي الأضلاع وكانت زواياه قائمة في ذلك الشكل يصبح مستطيلا.
- إذا كان شكل المستطيل أو شكل المعين معا في آن واحد في ذلك ينتج عنها شكل مربع.
قانون مساحة متوازي الأضلاع
متوازي الأضلاع واحد من الأشكال الهندسية صاحبة الأربعة أضلاع يوجد بها خطوط متوازية ومتساوية وتستطيع حساب مساحة متوازي المستطيلات عن طريق القانون التالي:
1- قانون مساحة متوازي الأضلاع باستخدام المساحة
- مساحة متوازي الأضلاع تساوي القاعدة في الارتفاع في أربعة.
- مثال إذا كانت القاعدة تساوى 5 سم والارتفاع يساوي 3 سم، ومساحه متوازي المستطيلات يساوي ثلاثة في خمسة يساوي خمسة عشر سنتيمتر مربع.
2- قانون متوازي الأضلاع بدون استخدام الارتفاع
- لو كانوا متوازي الأضلاع غير متعارف على الارتفاع الخاص به يمكن استخدام علم المثلثات حتى نستطيع أن نتعرف على مساحة متوازي الأضلاع.
- ذلك من خلال القانون التالي طول ضلع متوازي الأضلاع في الزاوية المحصورة.
3- قانون مساحة متوازي الأضلاع باستخدام الأقطار
- تستطيع معرفة مساحة متوازي الأضلاع باستخدام أطوال أقطار، وذلك من خلال القانون الثاني مساحه متوازي الأضلاع بتساوي طول القطر الأول في طول القطر الثاني.
مميزات متوازي الأضلاع
تمييز متوازي الأضلاع بمجموعة من الخواص ومن بينها ما يلي:
- إذا كان متوازي الأضلاع به ضلعين متقابلين متطابقين.
- إذا كان متوازي الأضلاع لديه زاويتين متقابلتين هم متطابقتين في الطول والقياس.
- إذا كان قطر متوازي الأضلاع في المنتصف فإنه يقسم الشكل إلى شكلين متساويين.
- إذا كان متوازي الأضلاع يوجد به زاويتين متقابلتين فهو متطابقتين في الطول.
- إذا كان متوازي المستطيلات على شكل مربع أو معين أو مستطيل تحمل مجموع زوايا هم 360 درجة.
معلومات هامه عن متوازي الأضلاع
متوازي الأضلاع من الأشكال الهندسية التي تحتوي على العديد من المعلومات الهامة وبعد عمل العديد من الأبحاث عليه توصلنا إلى الآتي:
- متوازي الأضلاع تستطيع حساب مساحته من خلال الارتفاع المقابلة في قطر الآخر.
- القطر في متوازي الأضلاع يقسم الشكل الهندسي إلى جزئين متساويين كل الزوايا المتواجدة في متوازي متقابلة الأضلاع متساوية في القياس.
- كل زاويتين متتاليتين أو متداخلتين يكون مجموع قياسهما 180 درجة.
- يعد المستطيل شكل من أشكال متوازي الأضلاع كل زاوية 90 درجة.
- متوازي المستطيلات من الأشكال الهندسية المتساوية في الطول.



